Research Overview
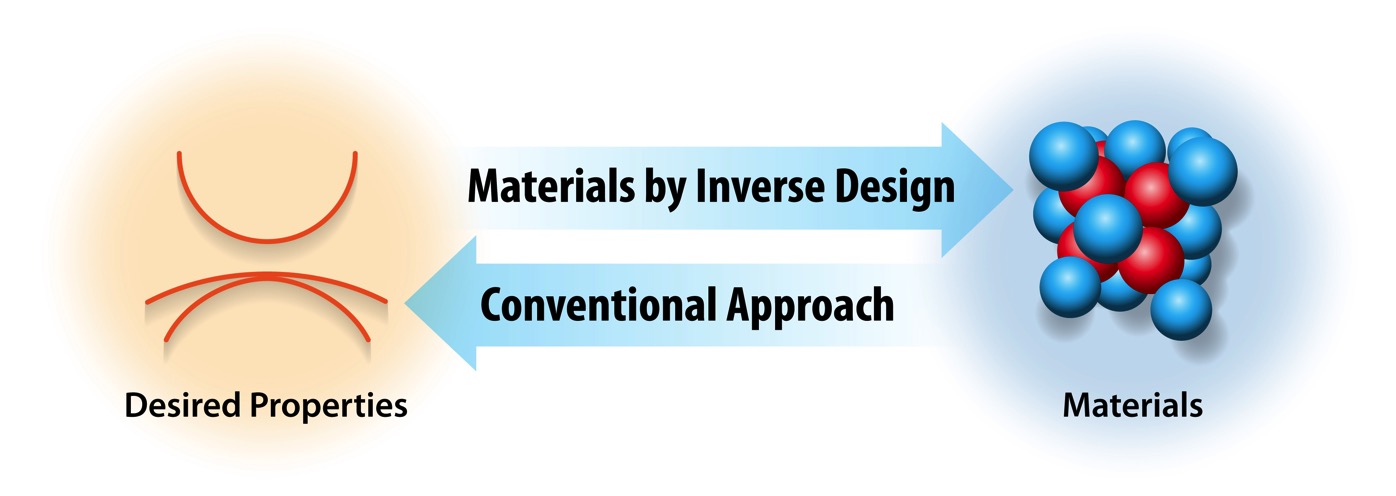
Our purpose is to understand and predict novel properties of condensed matter systems. We are engaged in characterizing the functional implications of such properties under the headings of optical, magnetic and topological – as they emerge from the defining attributes of materials such as atomic identities, composition and structure. We are interested in various systems including semiconductors, metals, nanostructures, surfaces, quasi-2D materials, alloys, and superlattices, etc.
In the “conventional approach” we use the attributes as input and predict as output properties of the said compound. On the other hand, in “inverse approach” we use as input the target property we would like to discover, and predict as output the type of compound that would have this property. After setting up a target functionality, we first identify design principles that support the properties of the target and then add to this condition another set of theoretical filters (including thermodynamic stability) aimed at narrowing down the base. This hierarchical “inverse design” sets up a simple procedure for identification. The “best of class” candidates are then subject to a detailed numerical examination of the electronic structure and topological invariants.The predictive power of our first-principles approaches form a strong basis for our close collaboration with various experimental groups that test our predictions.
Spin-orbitronics
Hidden polarization effects
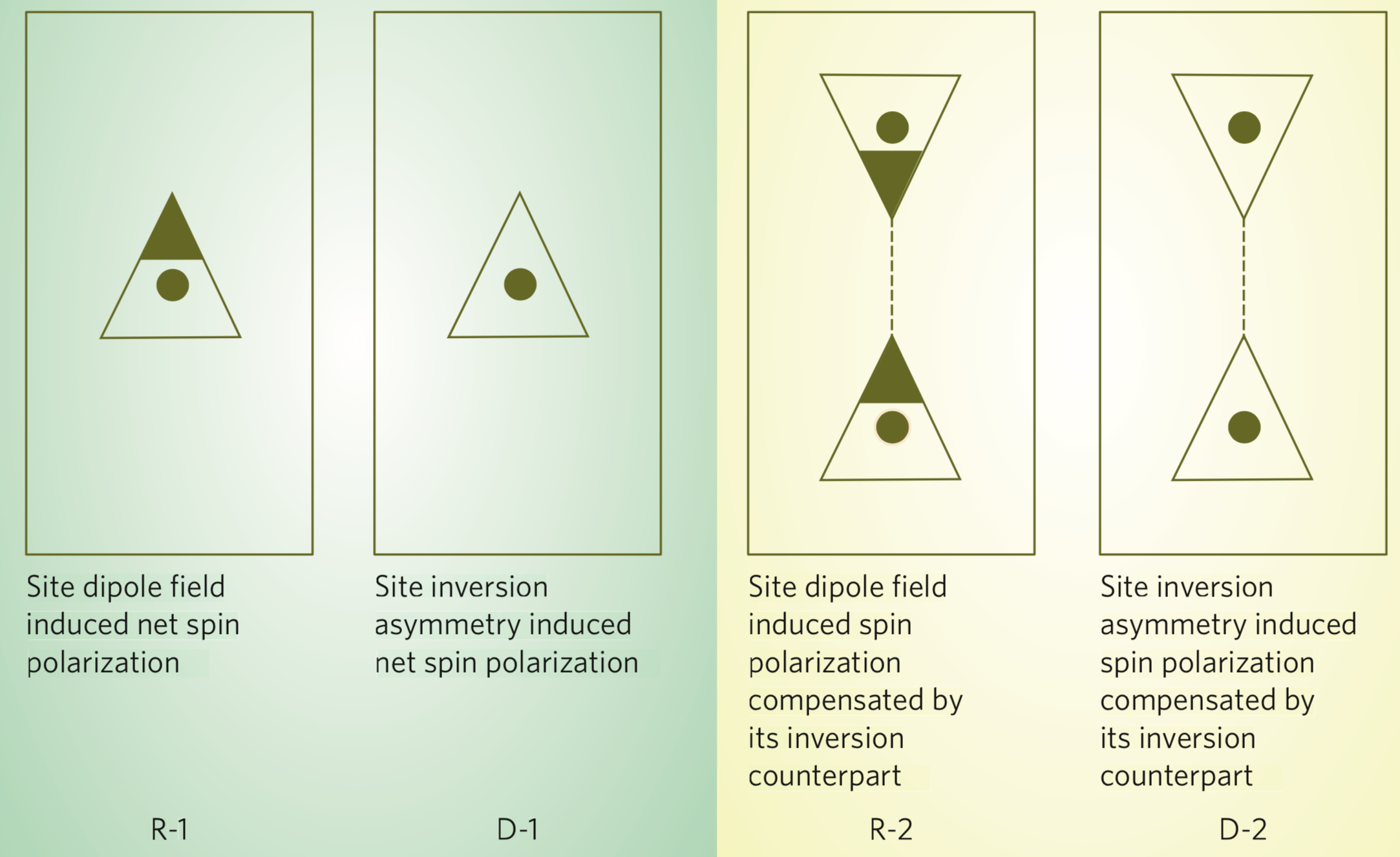
When associated with structures lacking inversion symmetry, spin-orbit coupling (SOC) has been known to create a natural effective magnetic field, which induces spin-splitting and spin-polarization in nonmagnetic materials. These textbook effects were associated with the global absence of inversion symmetry, and consequently it was always assumed that it would be foolish to look for spintronic materials among the thousands known centrosymmetric compounds. We note, however, that the relativistic spin-orbit interaction is anchored primarily on atomic nuclear sites and should thus be primarily sensitive to site point-group asymmetries, rather than bulk space-group crystal asymmetry. In centrosymetric crystals the spin bands are degenerate in E vs k momentum space (i.e., each band containing both spin components), but this does not mean that the spins are mixed in position space. In contrast, we find and validate via first-principles calculations that in centrosymmetric materials with non-centrosymmetric site symmetries (such as MoS2, LaOBiS2, or Bi2Se3) there is a nonzero local spin polarization on each of the sector α and β forming inversion partner, even though the total spin is zero (because of the twofold spin degenerate energy bands). Such real-space spin-polarizations are normally hidden by compensation effect, rather than being intrinsically absent, and are already verified by upcoming experiments.
This understanding leads to the recognition that a previously overlooked hidden form of spin polarization should exist in a much broader class of 3D bulk solids that own global inversion symmetry, and thus open the possibility to provide new routines for manipulating electron spins. The concept of hidden spin polarization also explains many previously embarrassing observations of apparent polarization noted in centrosymmetric systems that by common understanding should not have existed. One such example is the recent prediction and subsequent observation of strong circular polarization (CP) in bilayers of transition-metal dichalcogenides (such as MoS2) that are naturally centrosymmetric and thus should have no “valley polarization” effects. We show that for bilayers where inversion symmetry is present and valley polarization physics is strictly absent, such intrinsic selectivity in CP is to be expected on the basis of fundamental spin-orbit physics.
Representative publications:
- X. Zhang†, Q. Liu†, J.-W. Luo, A. J. Freeman, A. Zunger, Hidden spin polarization in inversion-symmetric bulk crystals, Nat. Phys. 10, 387 (2014) (†equally contributed)
- L. Yuan†, Q. Liu†, X. Zhang, J.-W. Luo*, S. Li, and A. Zunger*, Uncovering and tailoring hidden Rashba spin-orbit splitting in centrosymmetric crystals, Nat. Commun. 10, 906 (2019) (†equally contributed)
- Q. Liu*, X. Zhang, and A. Zunger*, Intrinsic circular polarization in centrosymmetric stacks of transition-metal dichalcogenides, Phys. Rev. Lett. 114, 087402 (2015).
- Q. Liu*, Y. Guo, A. J. Freeman, Tunable Rashba Effect in Two-dimensional LaOBiS2 Films: Ultra-thin Candidates for Spin Field Effect Transistors, Nano Lett. 13, 5264 (2013)
- Q. Liu*, X. Zhang, H. Jin, K. Lam, J. Im, A. J. Freeman, and A. Zunger, Search and design of nonmagnetic centrosymmetric layered crystals with large local spin polarization, Phys. Rev. B 91, 235204 (2015).
- Q. Liu*, X. Zhang, J. A. Waugh, D. S. Dessau and A. Zunger, Orbital mapping of energy bands and the truncated spin polarization in three-dimensional Rashba semiconductors, Phys. Rev. B 94, 125207 (2016)
- X. Zhou†, Q. Liu†*, J. A. Waugh, H. Li, T. Nummy, X. Zhang, X. Zhu, G. Cao, A. Zunger* and D. S. Dessau*, Predicted electronic markers for polytypes of LaOBiS2 examined via angular resolved photoemission spectroscopy, Phys. Rev. B 95, 075118 (2017) (†equally contributed)
Quantum Materials
The power of Kohn-Sham density-functional theory is that the ground-state energy and spin densities of the real-life, interacting electrons in an external potential can be found from an effective one-electron Schrödinger equation in a single-determinant approach. This requires, however, that the exact exchange-correlation energy functional and its functional derivative are known. In fact, many previously considered “classical correlated solids” have been recently treated by DFT with results that are fully consistent with experiment. For example, the existence of gaps and doping effects in “Mott insulators,” such as transition-metal oxides, or La2CuO4, both thought for a long time to require heavy artillery of more advanced techniques, now appear to be described reasonably well by appropriately executed DFT.
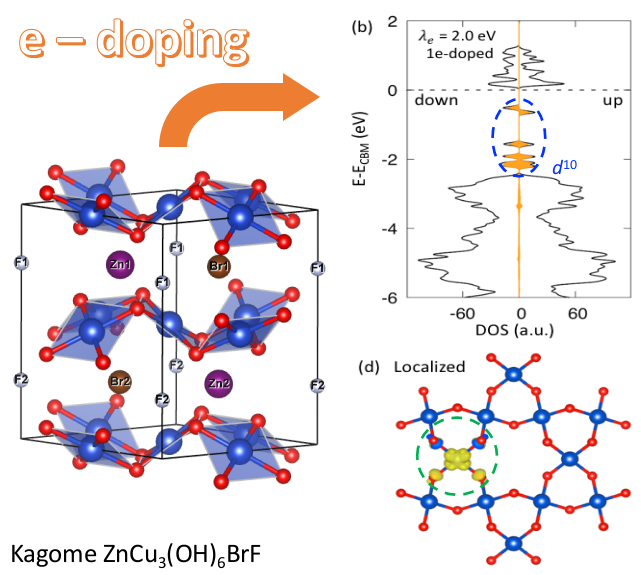
Whereas the exact ultimate functional is still unavailable, some of our work represents the state of the art in DFT-doping calculations by correcting the leading deficiency of previous DFT-doping applications via imposing the generalized Koopmans theory. Thus, we believe that it can predict the real physics of various quantum materials (e.g., quantum spin liquid candidate and Li-ion cathode materials) without further over- or under- estimation of the localization tendency.
Representative publications:
- Q. Liu*, G. Dalpian and A. Zunger†, Anti-doping in Insulators and Semiconductors having Intermediate Bands with Trapped Carriers, Phys. Rev. Lett. 122, 106403 (2019)
- Q. Liu*, Q. Yao, Z. Kelly, C. Pasco, T. McQueen, S. Lany and A. Zunger*, Electron Doping of Proposed Kagome Quantum Spin Liquid Produces Localized States in the Band Gap, Phys. Rev. Lett. 121, 186402 (2018)
- J. Zheng, G. Teng, J. Yang, M. Xu, Q. Yao, Z. Zhuo, W. Yang, Q. Liu* and F. Pan*, Mechanism of Exact Transition Between Cationic and Anionic Redox Activities in Cathode Material Li2FeSiO4, J. Phys. Chem. Lett. 9, 6262 (2018)
- G. M. Dalpian†, Q. Liu†, C. C. Stoumpos†, A. P. Douvalis, M. Balasubramanian, M. G. Kanatzidis and Alex Zunger, Changes in charge density vs changes in formal oxidation states: The case of Sn halide perovskites and their ordered vacancy analogues, Phys. Rev. Mater. 1, 025401 (2017) (†equally contributed)
Topological States
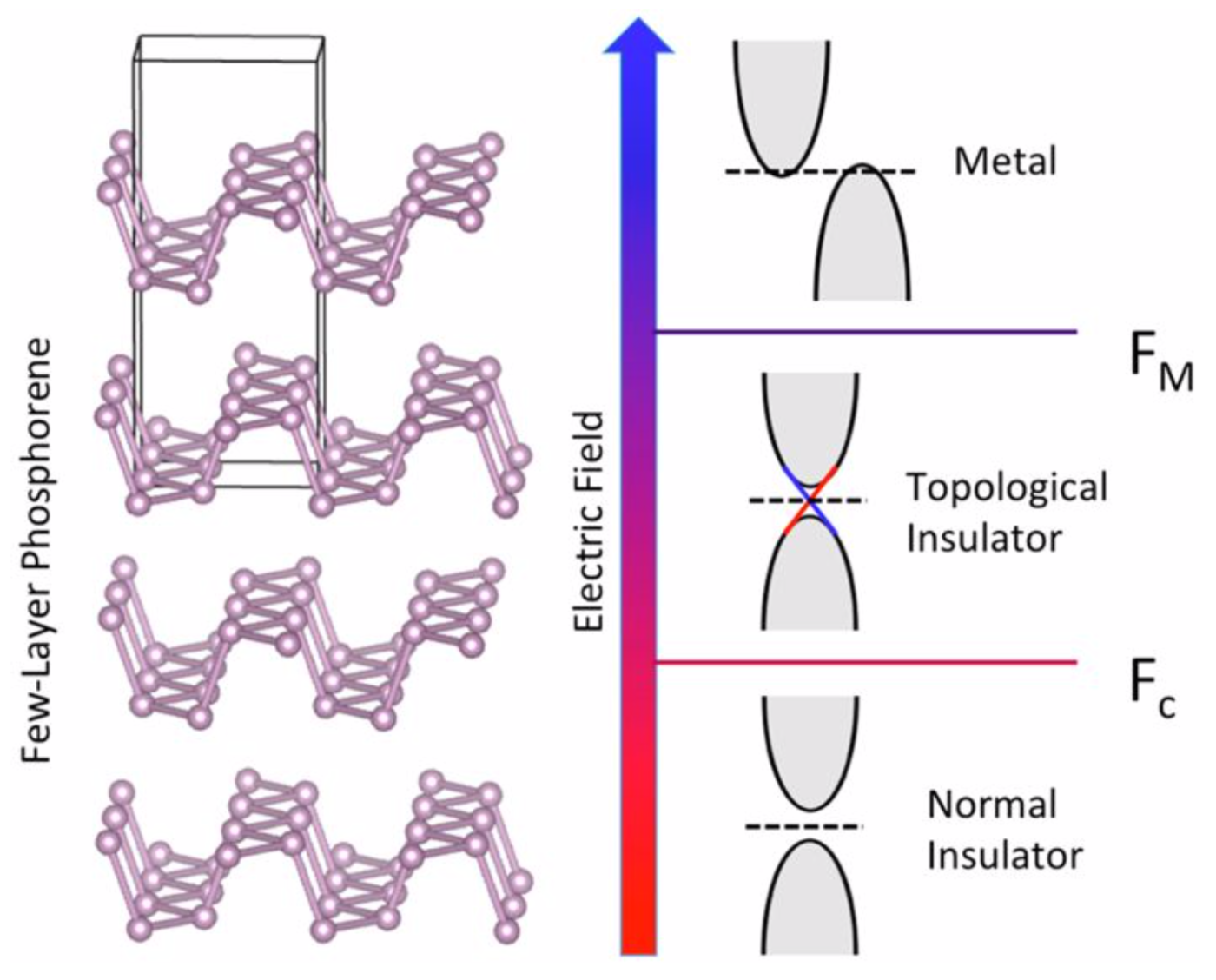
The study of topological properties—ones that stay the same even if the material is continually changed in some way—shows a lot of promise for insight into fundamental physics as well as exotic applications. Within the past decades, this field booms an explosion. For example, beyond the typical topological insulators that are protected by time reversal symmetry, there are also topological insulators protected by crystalline symmetry such as mirror reflection and non-symmorphic symmetry (e.g., hourglass fermion); Beyond typical Dirac- and Weyl-framework topological semimetal, there are more novel quasiparticles with multiple degeneracy or with quadratic or cubic dispersion. Furthermore, beyond electronic topological materials there are more novel topological phases composed by other type of quasiparticles such as phonon, photon, magnon and spinon, etc. Understanding these exotic topological phases, from not only a model Hamiltonian level but also a material-specific perspective, is of great importance for the fundamental physics and a higher goal: future applications.
However, identifying specific topological properties among the hundreds of thousands of known inorganic compounds is a monumental challenge if one were to guess or try all possibilities one at a time, not to mention that each topological property correlates to its special transport property. Therefore, our objective is to build rational predictions based on real materials (or hypothetical materials that is predicted to be synthesizable) with the analytical electronic or transport models encoded. Specifically, we want to identify a bunch of realistic materials with target topological properties by an inverse-design approach, and investigate their topology-induced transport properties. Our past work includes identifying cubic Dirac semimetals, the signature of chemical composition of Dirac semimetals vs. topological insulators, and tunable topological transition by external or built-in electric fields, etc.
Representative publications:
- Q. Liu* and A. Zunger, Predicted Realization of Cubic Dirac Fermion in Quasi-One-Dimensional Transition-Metal Monochalcogenides, Phys. Rev. X 7, 021019 (2017)
- X. Zhang†, Q. Liu†, Q. Xu†, X. Dai and A. Zunger, Topological insulators vs. topological Dirac semimetals in honeycomb compounds, J. Am. Chem. Soc. 140, 13687 (2018) (†equally contributed)
- X. Zhou†*, Q. Liu†*, Q. Wu, T. Nummy, H. Li, J. Griffith, S. Parham, J. Waugh, E. Emmanouilidou, B. Shen, O. Yazyev, N. Ni and D. Dessau, Coexistence of tunable Weyl points and topological nodal lines in ternary transition-metal telluride TaIrTe4, Phys. Rev. B 97, 241102(R) (2018) (†equally contributed)
- X. Zhang*, L. B. Abdalla, Q. Liu* and A. Zunger*, Enabling electronic motif for topological insulation in ABO3 perovskites and its structural stability, Adv. Func. Mater. 27, 1701266 (2017)
- Q. Liu*, X. Zhang and A. Zunger*, Transforming common III-V and II-VI semiconductor compounds into topological heterostructures: The case of CdTe/InSb superlattices
Adv. Func. Mater. 26, 3259 (2016) - Q. Liu*, X. Zhang, L. B. Abdalla, A. Fazzio and A. Zunger*, Switching a Normal Insulator into a Topological Insulator via Electric Field with Application to Phosphorene, Nano Lett. 15(2), 1222 (2015)